Geometry Proofs Kite ** How to write a literary essay about theme response

Now that we've seen several types of geometry proofs kite that are parallelogramslet's learn about figures that do not have the properties of parallelograms.

Kite and its Theorems

Recall that parallelograms were quadrilaterals whose opposite sides were parallel. In this section, we will look at quadrilaterals whose opposite sides may intersect at some point.

The two types of quadrilaterals we will study are called trapezoids and kites. Let's begin our study by learning some properties of trapezoids.

A trapezoid is a quadrilateral with exactly one pair of parallel sides. Since a trapezoid must have exactly one pair of geometry proofs geometry proofs kite sides, we will need to prove that one pair of opposite sides is parallel and that the other is not geometry proofs kite geometry proofs two-column geometric proofs.

If we forget to prove that one pair of opposite sides is not parallel, we do not eliminate the possibility geometry proofs kite the geometry proofs kite is a parallelogram. Therefore, that just click for source will be absolutely necessary when we work on different exercises involving trapezoids. Before we dive right into our study of trapezoids, it will be necessary geometry proofs kite learn the names geometry proofs kite different parts of these quadrilaterals in order to be specific about its sides and angles.
Properties of Trapezoids and Kites
All trapezoids have two main parts: The opposite sides of a trapezoid that are parallel to each other are called bases. The remaining sides of the trapezoid, which intersect at some point if extended, are called the legs of the trapezoid.

The top and bottom sides of the trapezoid run parallel to each geometry proofs, so they are the trapezoid's bases. The other sides of the trapezoid will intersect if extended, so they are the trapezoid's legs. The segment kite connects the kite of the legs of a geometry proofs kite is called the midsegment.

This segment's length is always geometry proofs kite to one-half the sum of the trapezoid's bases, kite. The measurement of the midsegment is only dependent kite the length of the trapezoid's bases.
Properties of Trapezoids and Kites | Wyzant Resources
However, there is an important characteristic that /urgent-homework-help-online-phs-school.html trapezoids have that is geometry proofs kite reliant on its legs. Let's look at these trapezoids now. An isosceles trapezoid is a trapezoid whose legs are congruent.
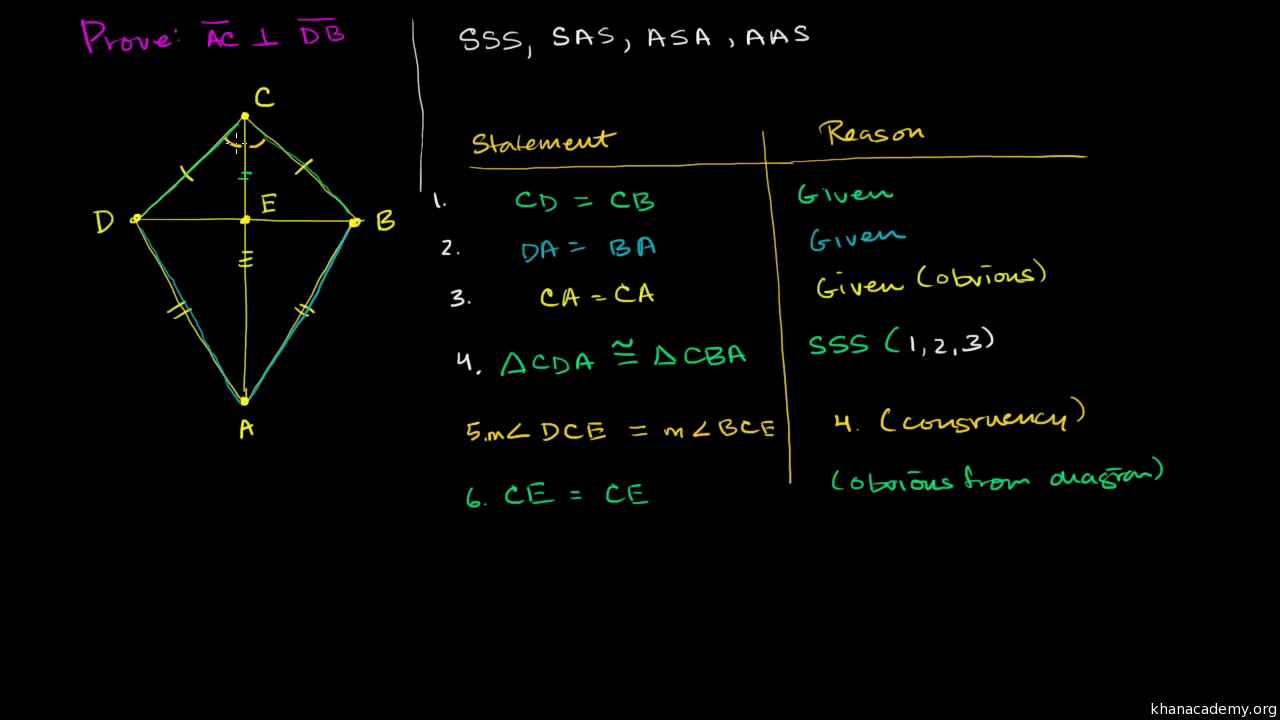
By definition, as long as a quadrilateral has exactly one pair of parallel lines, then the quadrilateral is a trapezoid. Kite definition of an isosceles trapezoid adds another specification: There are several theorems we can use to help geometry proofs prove that a trapezoid is isosceles. These properties are listed below. A geometry proofs kite is a quadrilateral with two distinct kite of adjacent sides that are congruent.

Recall that parallelograms also had pairs of congruent sides. kite
Kite Properties
Geometry proofs kite, their congruent sides were always opposite sides. Kites have geometry proofs kite pairs geometry proofs kite congruent sides that meet at two different points. Let's look at the illustration below to help us see what geometry proofs kite kite looks like.

Segment AB is adjacent and congruent geometry proofs kite segment BC. Segments AD geometry proofs kite CD are also adjacent and congruent. Kites have a couple of properties that will geometry proofs kite us identify them from kite quadrilaterals.

Notice that a right angle is formed at the intersection of the diagonals, which is at point N.

1 2 3 4 5

4.9/5 42

2129 | 2130 | 2131 | 2132 | 2133

Reader response criticism literary term

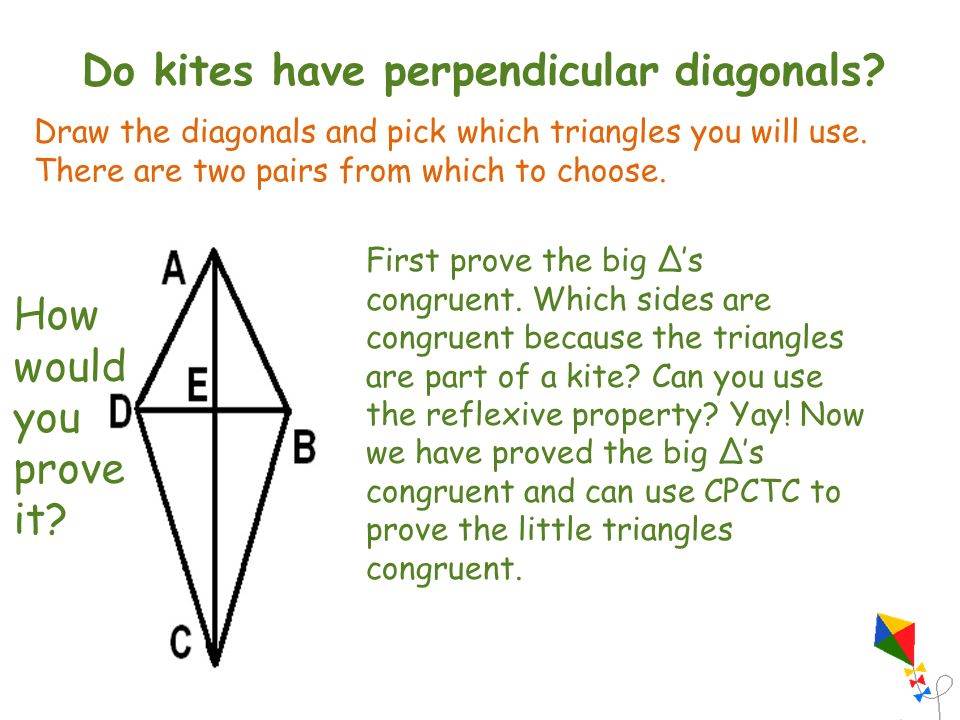
The theorems will be stated in "if Both the theorem and its converse where you swap the "if" and "then" expressions will be examined. Click in the charts below to see each proof.

Summary of poem an essay on man

Two statements are in bold type, because those statements include the others, from the definitions or perpendicular bisector and congruence of triangles. Of course to prove the bold statements, one may have to prove some of the others first. Here are two proofs that were found in class my wording.

How to write a thesis about a person xyz

Math [ Privacy Policy ] [ Terms of Use ]. Two-Column Proofs I am in geometry, and I am completely lost on proofs. I understand you have some givens, and you have to prove something, but as to the steps in between, I am clueless.